ofstream的使用方法似乎以前在一篇文章里面看到过，今天拿出来复习一下吧 ofstream是从内存到硬盘，ifstream是从硬盘到内存，其实所谓的流缓冲就是内存空间;
在C++中，有一个stream这个类，任何的I/O都以这个“流”类为基础的，包括我们要认识的文档I/O，stream这个类有两个重要的运算符：
1、插入器(<<)
　　向流输出数据。比如说系统有一个默认的标准输出流(cout)，一般情况下就是指的显示器，所以，cout<</"Write Stdout/"<<’//n’;就表示把字符串/"Write Stdout/"和换行字符(’//n’)输出到标准输出流。
2、析取器(>>)
　　从流中输入数据。比如说系统有一个默认的标准输入流(cin)，一般情况下就是指的键盘，所以，cin>>x;就表示从标准输入流中读取一个指定类型(即变量x的类型)的数据。
　　在C++中，对文档的操作是通过stream的子类fstream(file stream)来实现的，所以，要用这种方式操作文档，就必须加入头文档fstream.h。下面就把此类的文档操作过程一一道来。
一、打开文档
　　在fstream类中，有一个成员函数open()，就是用来打开文档的，其原型是：
void open(const char* filename,int mode,int access);
参数：
filename：　　要打开的文档名
mode：　　　　要打开文档的方式
access：　　　打开文档的属性
打开文档的方式在类ios(是任何流式I/O类的基类)中定义，常用的值如下：
ios::app：　　　以追加的方式打开文档
ios::ate：　　　文档打开后定位到文档尾，ios:app就包含有此属性
ios::binary：　以二进制方式打开文档，缺省的方式是文本方式。两种方式的区分见前文
ios::in：　　　 文档以输入方式打开（文档数据输入到内存）
ios::out：　　　文档以输出方式打开（内存数据输出到文档）
ios::nocreate： 不建立文档，所以文档不存在时打开失败
ios::noreplace：不覆盖文档，所以打开文档时假如文档存在失败
ios::trunc：　　假如文档存在，把文档长度设为0
　　能够用“或”把以上属性连接起来，如ios::out|ios::binary
　　打开文档的属性取值是：
0：普通文档，打开访问
1：只读文档
2：隐含文档
4：系统文档
　　能够用“或”或“+”把以上属性连接起来，如3或1|2就是以只读和隐含属性打开文档。
　　例如：以二进制输入方式打开文档c://config.sys
fstream file1;
file1.open(/"c:////config.sys/",ios::binary|ios::in,0);
　　假如open函数只有文档名一个参数，则是以读/写普通文档打开，即：
file1.open(/"c:////config.sys/"); <=> file1.open(/"c:////config.sys/",ios::in|ios::out,0);
　　另外，fstream更有和open()相同的构造函数，对于上例，在定义的时侯就能够打开文档了：
fstream file1(/"c:////config.sys/");
　　特别提出的是，fstream有两个子类：ifstream(input file stream)和ofstream(outpu file stream)，ifstream默认以输入方式打开文档，而ofstream默认以输出方式打开文档。 [Page]
ifstream file2(/"c:////pdos.def/");//以输入方式打开文档
ofstream file3(/"c:////x.123/");//以输出方式打开文档
　　所以，在实际应用中，根据需要的不同，选择不同的类来定义：假如想以输入方式打开，就用ifstream来定义；假如想以输出方式打开，就用ofstream来定义；假如想以输入/输出方式来打开，就用fstream来定义。
二、关闭文档
　　打开的文档使用完成后一定要关闭，fstream提供了成员函数close()来完成此操作，如：file1.close();就把file1相连的文档关闭。
三、读写文档
　　读写文档分为文本文档和二进制文档的读取，对于文本文档的读取比较简单，用插入器和析取器就能够了；而对于二进制的读取就要复杂些，下要就周详的介绍这两种方式
　　1、文本文档的读写
　　文本文档的读写很简单：用插入器(<<)向文档输出；用析取器(>>)从文档输入。假设file1是以输入方式打开，file2以输出打开。示例如下：
　　file2<</"I Love You/";//向文档写入字符串/"I Love You/"
　　int i;
　　file1>>i;//从文档输入一个整数值。
　　这种方式更有一种简单的格式化能力，比如能够指定输出为16进制等等，具体的格式有以下一些
操纵符 功能 输入/输出
dec 格式化为十进制数值数据 输入和输出
endl 输出一个换行符并刷新此流 输出
ends 输出一个空字符 输出
hex 格式化为十六进制数值数据 输入和输出
oct 格式化为八进制数值数据 输入和输出
setpxecision(int p) 配置浮点数的精度位数 输出
　　比如要把123当作十六进制输出：file1<<hex<<123;要把3.1415926以5位精度输出：file1<<setpxecision(5)<<3.1415926。
　　2、二进制文档的读写
①put()
　　put()函数向流写入一个字符，其原型是ofstream &put(char ch)，使用也比较简单，如file1.put(’c’);就是向流写一个字符’c’。
②get()
　　get()函数比较灵活，有3种常用的重载形式：
　　一种就是和put()对应的形式：ifstream &get(char &ch);功能是从流中读取一个字符，结果保存在引用ch中，假如到文档尾，返回空字符。如file2.get(x);表示从文档中读取一个字符，并把读取的字符保存在x中。
　　另一种重载形式的原型是： int get();这种形式是从流中返回一个字符，假如到达文档尾，返回EOF，如x=file2.get();和上例功能是相同的。
　　更有一种形式的原型是：ifstream &get(char *buf,int num,char delim=’//n’)；这种形式把字符读入由 buf 指向的数组，直到读入了 num 个字符或碰到了由 delim 指定的字符，假如没使用 delim 这个参数，将使用缺省值换行符’//n’。例如：

//做啦好久老是WA，不知到为什么，刚刚开始吧他们都设成是双浮点型，老是过不了；改成整形就过啦；

//后来又是超时，吧cin改成scanf();果断过！！！！！

#include<stdio.h>
#include<queue>
#include<iostream>
#include<string.h>
#include<math.h>
using namespace std;
#define eps 1e-6
const int MAXN=3005;
const int INF=1<<28;
int g[MAXN][MAXN],Mx[MAXN],My[MAXN],Nx,Ny;int dx[MAXN],dy[MAXN],dis;
bool vst[MAXN];
struct Node1{
    int x,y,s;
}guests[MAXN];
struct Node2{
    int x,y;
}um[MAXN];
double distance(Node1 a,Node2 b){
    double x=a.x-b.x; 
    double y=a.y-b.y;   
    return sqrt(x*x+y*y);
} 
bool searchP(void){
    queue<int> Q;
    dis = INF;
    memset(dx, -1, sizeof(dx));
    memset(dy, -1, sizeof(dy));
    for (int i = 0; i < Nx; i++)
        if (Mx[i] == -1){
            Q.push(i); dx[i] = 0;
        }
        while (!Q.empty()) {
            int u = Q.front(); Q.pop();
            if (dx[u] > dis) break;
            for (int v = 0; v < Ny; v++)
                if (g[u][v] && dy[v] == -1) {
                    dy[v] = dx[u]+1;
                    if (My[v] == -1) dis = dy[v];
                    else{
                        dx[My[v]] = dy[v]+1;
                        Q.push(My[v]);
                    }
                }
        }
        return dis != INF;
}
bool DFS(int u){
    for (int v = 0; v < Ny; v++)
        if (!vst[v] && g[u][v] && dy[v] == dx[u]+1) {
            vst[v] = 1;
            if (My[v] != -1 && dy[v] == dis) continue;
            if (My[v] == -1 || DFS(My[v])) {
                My[v] = u; Mx[u] = v;
                return 1;
            }
        }
        return 0;
}
int MaxMatch(void){
    int res = 0;
    memset(Mx, -1, sizeof(Mx));
    memset(My, -1, sizeof(My));
    while (searchP()) {
        memset(vst, 0, sizeof(vst));
        for (int i = 0; i < Nx; i++)
            if (Mx[i] == -1 && DFS(i)) res++;
    }
    return res;
}
int main(){
    //freopen("test.in","r",stdin);
    //freopen("test.out","w",stdout);   
    int n,m,t,i,j;   
    int T,iCase=0;  
    scanf("%d",&T); 
    while(T--)   
    {     
        iCase++;    
        scanf("%d",&t); 
        scanf("%d",&m);   
        for(i=0;i<m;i++)      
            scanf("%d%d%d",&guests[i].x,&guests[i].y,&guests[i].s);   
        scanf("%d",&n);     
        for(i=0;i<n;i++)    
            scanf("%d%d",&um[i].x,&um[i].y);
        Nx=m;Ny=n;      
        memset(g,0,sizeof(g));    
        for(i=0;i<m;i++)    
        {           
            for(j=0;j<n;j++) 
            {             
                if(distance(guests[i],um[j])/guests[i].s-t<eps)    
                {                
                    g[i][j]=1;       
                }       
            }       
        }           
        printf("Scenario #%d:\n%d\n\n",iCase,MaxMatch());  
    }   
    return 0;
}      

//hash判重
//好孩子；
//hdu1429利用二进制的&和|运算：
#include<iostream>
#include<queue>
using namespace std;
const int T = 22;
char g[T][T];
int vis[T][T][1030],n,m,t,ans;
int dir[4][2]={0,1,1,0,0,-1,-1,0};

struct point{
    int x;
    int y;
    int step;
    int key;
};
point s;

void inset(){
    for(int i=0;i<n;i++){
        cin>>g[i];
        for(int j=0;j<m;j++){
            if(g[i][j]=='@'){
                s.x=i;
                s.y=j;
                s.key=0;
                s.step=0;
            }
        }
    }
}


void bfs(){
    queue<point>  Q;
    point tp;
    ans=-1;
    memset(vis,0,sizeof(vis));
    vis[s.x][s.y][s.key]=1;
    Q.push(s);
    while(!Q.empty()){
         tp=Q.front();Q.pop();
         for(int k=0;k<4;k++){
             s=tp;
             s.x=tp.x+dir[k][0];
             s.y=tp.y+dir[k][1];
             if(s.x>=0 && s.x<n && s.y>=0 && s.y<m && g[s.x][s.y]!='*' && !vis[s.x][s.y][s.key]){
                 if(g[s.x][s.y]=='.' || g[s.x][s.y]=='@'){
                       vis[s.x][s.y][s.key]=1;
                       s.step+=1;
                       Q.push(s);
                       //cout<<s.x<<" "<<s.y<<endl;
                 }
                 if(g[s.x][s.y]=='^'){
                     if(s.step+1<t) ans=s.step+1;
                     return ;
                 }
                 if(g[s.x][s.y]>='A' && g[s.x][s.y]<='J'){
                      int key=1<<(g[s.x][s.y]-'A');
                      if(s.key & key){
                           vis[s.x][s.y][s.key]=1;
                           s.step+=1;
                           Q.push(s);
                          //cout<<s.x<<" "<<s.y<<endl;
                      }
                 }
                 if(g[s.x][s.y]>='a' && g[s.x][s.y]<='j'){
                       int key=1<<(g[s.x][s.y]-'a');
                       if(!vis[s.x][s.y][s.key|key]){
                            vis[s.x][s.y][s.key|key]=1;
                            s.step+=1;s.key=s.key|key;
                            Q.push(s);
                            //cout<<s.x<<" "<<s.y<<endl;
                       }
                 }
             }
         }
    }
}


int main(){

    while(cin>>n>>m>>t){
        inset();
        bfs();
        cout<<ans<<endl;
    }

    return 0;
}

//hdu 3336
//Answer 好孩子
//刚刚思想是采用KMP+DP的递推；前1—next[i]与后面next[i]—i-1刚刚好相等
//这个就在前面的基础上加一代表前i-1个为前最的最大重复数；
//思路是next[]数组总体往后移一位；

就像：abcdabcd;

next[]:

-1 0 0 0 0 1 1 1 1

后移一位：
0 0 0 0 1 1 1 1

刚刚好对应字符下表看成是1开始的每一位：
//状态方程：cont[i]=cont[next[i]]+1;
//本题就是把所有的cont[]加起来；
#include<iostream>
using namespace std;

const int T=300000;
const int size=10007;

int next[T],cont[T],len;
char a[T];

void getnext(){
 int i,j;
 next[0]=-1;i=0;j=-1;
 while(i<len){
  if(j==-1 || a[i]==a[j]){
   i++;
   j++;
   next[i]=j;
  }
  else j=next[j];
 }
}

//dp
int Gram(){
 int i,sum=0;
 memset(cont,0,sizeof(cont));
 for(i=1;i<=len;i++){
  cont[i]=(cont[next[i]]+1)%size;  //前缀i的相等加一；
  sum=(sum+cont[i])%size;
 }
 return sum;
}

int main(){
 int R;
 freopen("in.txt","r",stdin);
 freopen("out.txt","w",stdout);
 cin>>R;while(R--){
  cin>>len;
  cin>>a;
  getnext();
  int sum=Gram();
  cout<<sum<<endl;
 }
 return 0;
}

KM 算法:

#include <iostream>
#include <cstdio>
using namespace std;
int const MAXN = 250;
int graph[MAXN][MAXN], cnt[MAXN];
//邻接表矩阵，点度
bool ck[MAXN];//记录是否被访问
int match[MAXN];//匹配数组，记录右端到左端的匹配
int V, E;//点数、边数
bool search(int G[][MAXN], int k)
{//找增广边
    for(int i = 0; i < cnt[k]; i++)
    {
        int p = G[k][i];
        if(ck[p])
        {
            ck[p] = false;
            int t = match[p];
            if(t == -1 || search(G, t) )
            {
                match[p] = k;
                return true;
            }
            //match[p] = t;
        }
    }
    return false;
}

int hungary(int G[][MAXN], int left)
{//传入矩阵和左端点数，传出匹配的对数
    int answer(0);
    int i, j;
    for(i = 0; i < V; i++)        // V为右端顶点数
    {
        match[i] = -1;
    }
    for(i = 0; i < left; i++)
    {
       for(j = 0; j < V; j++)
       {
            ck[j] = true;
        }
       if(search(G, i))
       {
            ++answer;
       }
    }
    return answer;
}

 

/**********************************************
二分图匹配（Hopcroft-Carp的算法）。
初始化：g[][]邻接矩阵
调用：res=MaxMatch();  Nx,Ny要初始化！！！
时间复杂大为 O(V^0.5 E)

适用于数据较大的二分匹配 
***********************************************/ 
const int MAXN=3001;
const int INF=1<<28;
int g[MAXN][MAXN],Mx[MAXN],My[MAXN],Nx,Ny;
int dx[MAXN],dy[MAXN],dis;
bool vst[MAXN];
bool searchP()
{
    queue<int>Q;
    dis=INF;
    memset(dx,-1,sizeof(dx));
    memset(dy,-1,sizeof(dy));
    for(int i=0;i<Nx;i++)
        if(Mx[i]==-1)
        {
            Q.push(i);
            dx[i]=0;
        }  
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        if(dx[u]>dis)  break;
        for(int v=0;v<Ny;v++)
            if(g[u][v]&&dy[v]==-1)
            {
                dy[v]=dx[u]+1;
                if(My[v]==-1)  dis=dy[v];
                else
                {
                    dx[My[v]]=dy[v]+1;
                    Q.push(My[v]);
                }    
            }    
    }  
    return dis!=INF;    
}    
bool DFS(int u)
{
    for(int v=0;v<Ny;v++)
       if(!vst[v]&&g[u][v]&&dy[v]==dx[u]+1)
       {
           vst[v]=1;
           if(My[v]!=-1&&dy[v]==dis) continue;
           if(My[v]==-1||DFS(My[v]))
           {
               My[v]=u;
               Mx[u]=v;
               return 1;
           }    
       }  
    return 0;  
}
int MaxMatch()
{
    int res=0;
    memset(Mx,-1,sizeof(Mx));
    memset(My,-1,sizeof(My));
    while(searchP())
    {
        memset(vst,0,sizeof(vst));
        for(int i=0;i<Nx;i++)
          if(Mx[i]==-1&&DFS(i))  res++;
    }
    return res;   
}    
    

关于图论中一些名称的介绍：

独立集：

    独立集是指图的顶点集的一个子集,该子集的导出子图不含边.如果一个独立集不是任何一个独立集的子集, 那么称这个独立集是一个极大独立集.一个图中包含顶点数目最多的独立集称为最大独立集。最大独立集一定是极大独立集，但是极大独立集不一定是最大的独立集。

支配集：

    与独立集相对应的就是支配集，支配集也是图顶点集的一个子集，设S 是图G 的一个支配集，则对于图中的任意一个顶点u，要么属于集合s, 要么与s 中的顶点相邻。 在s中除去任何元素后s不再是支配集，则支配集s是极小支配集。称G的所有支配集中顶点个数最 少的支配集为最小支配集，最小支配集中的顶点个数成为支配数。

最小点的覆盖：

   最小点的覆盖也是图的顶点集的一个子集，如果我们选中一个点，则称这个点将以他为端点的所有边都覆盖了。将图中所有的边都覆盖所用顶点数最少，这个集合就是最小的点的覆盖。

最大团：

    图G的顶点的子集，设D是最大团，则D中任意两点相邻。若u，v是最大团，则u,v有边相连，其补图u,v没有边相连，所以图G的最大团=其补图的最大独立集。

一些性质：

最大独立集+最小覆盖集=V

最大团=补图的最大独立集

最小覆盖集=最大匹配

问题提出：已知数组a[],元素个数为n,现在更改a中的元素,要求得新的a数组中i到j区间内的和(1<=i<=j<=n).

思考：对于这个问题,我们可以暴力地来解决,从a[i]一直累加到a[j],最坏的情况下复杂度为O(n),对于m次change&querry,合起来的复杂度为O(m*n),在n或m很大的情况下,这样的复杂度是让人无法忍受的.另外,如果没有元素的变更,我们完全可以存储sum[1,k](k=1,2,……),然后对任意给定的查找区间[i,j],都可以方便的用ans=sum[1,j]-sum[1,i-1],当然这只是没有元素改变的情况下的比较优化的解法.那么对于有元素变更的问题是否有更高效的方法呢?(废话!没有我还写啥?!)可以想一下,每次更改的元素是比较少的,有时候甚至每次只改变一个元素,但是在用暴力方法求区间和的时候,却对区间内所有的元素都累加了一遍,这样其实造成了许多无谓的运算.这时候也许会想到如果能把一些结果存起来会不会减少很多运算?答案是肯定的,但问题是怎么存,存什么?如果存任意区间的话,n比较大的时候不但内存吃不消,而且存储的量太大,不易更改,反而得不偿失;那么也许可以考虑存储特定的一些区间(比如说线段树,其实现在讨论的问题用线段树完全可以解,以后再详细写线段树).那么现在重新回过头来,看下这个问题,我们已经确定了要存储一些特定区间sum的想法,接下来我们要解决的无非是两个问题:1、减少更改元素后对这些区间里的sum值的更改时间.2、减少查找的时间.

好了废话了这么半天,无非是想让自己以及看到的人明白为什么要用树状数组.

接下来正式入题.

首先我们可以借鉴元素不变更问题的优化方法,先得到前i-1项之和and前j项之和,以s[i]表示前i项之和,那么sum[i,j]=s[j]-s[i-1].那么现在的问题已经转化为求前i项之和了.另外,我们已经确定要存储一些特定区间的和,现在就要来揭示这些特定的区间究竟指什么.

在文字说明之前先引入一个非常经典的,在网上找到的树状数组文章里几乎都要出现的一个图片

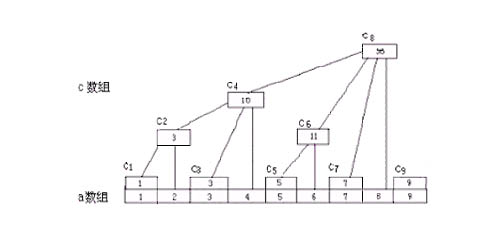
从图中不难发现,c[k]存储的实际上是从k开始向前数k的二进制表示中右边第一个1所代表的数字个元素的和(这么说可能有点拗口,令lowbit为k的二进制表示中右边第一个1所代表的数字,然后c[k]里存的就是从a[k]开始向前数lowbit个元素之和)这么存有什么好处呢?无论是树状数组还是线段树,都用到了分块的思想,而树状数组采用这样的存储结构我想最主要的还是这样方便计算,我们可以用位运算轻松地算出lowbit.分析一下这样做的复杂度:对于更改元素来说,如果第i个元素被修改了,因为我们最终还是要求和,所以可以直接在c数组里面进行相应的更改,如图中的例子,假设更改的元素是a[2],那么它影响到得c数组中的元素只有c[2],c[4],c[8],我们只需一层一层往上修改就可以了,这个过程的最坏的复杂度也不过O(logN);对于查找来说,如查找s[k],只需查找k的二进制表示中1的个数次就能得到最终结果,比如查找s[7],7的二进制表示中有3个1,也就是要查找3次,到底是不是呢,我们来看上图,s[7]=c[7]+c[6]+c[4],可能你还不知道怎么实现这个过程.

还以7为例,二进制为0111,右边第一个1出现在第0位上,也就是说要从a[7]开始向前数1个元素(只有a[7]),即c[7];

然后将这个1舍掉,得到6,二进制表示为0110,右边第一个1出现在第1位上,也就是说要从a[6]开始向前数2个元素(a[6],a[5]),即c[6];

然后舍掉用过的1,得到4,二进制表示为0100,右边第一个1出现在第2位上,也就是说要从a[4]开始向前数4个元素(a[4],a[3],a[2],a[1]),即c[4].

代码实现:

Code
int lowbit(int x)//计算lowbit
{
    return x&(-x);
}
void add(int i,int val)//将第i个元素更改为val
{
    while(i<=n)
    {
        c[i]+=val;
        i+=lowbit(i);
    }
}
int sum(int i)//求前i项和
{
    int s=0;
    while(i>0)
    {
        s+=c[i];
        i-=lowbit(i);
    }
    return s;
}

字符串匹配算法:KMP学习心得

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。

#include<iostream>
using namespace std;
int a[1000010],b[10010],next[10010];
int lena,lenb;

void inset()
{
    int i;
    scanf("%d%d",&lena,&lenb);
    for(i=0;i<lena;i++)
        scanf("%d",&a[i]);
    for(i=0;i<lenb;i++)
        scanf("%d",&b[i]);
}




void Gurm()
{
    int j=0,k=-1;
    next[0]=-1;
    while(j<lenb)
    {
        if(k==-1 || b[j]==b[k])
        {
            ++j;
            ++k;
            next[j]=k;
        }
        else
        {
            k=next[k];
        }
    }
}



int kmp()
{
    int i=0,j=0;
    Gurm();
    while(i<lena && j<lenb)
    {
        if(j==-1 || a[i]==b[j] )
        {
            i++;
            j++;
        }
        else
        {
            j=next[j];
        }
    }
    if(j<lenb)  return -1;
    else return i-j+1;
}





int main()
{
    //freopen("D:\\in.txt","r",stdin);
    int R;scanf("%d",&R);
    while(R--)
    {
        inset();
        printf("%d\n",kmp());
    }
    return 0;
}
 

KMP:next[]的应用。

 * 一般next[i]与优化next[i]的区别：

 *如果模式串p下标为i的字符（字符第一个的下标为0）的前k个字符与开头前k个字符相等（0=<k<i 注意这里没有等于i）

 *     对于一般的next[i]，不管p[i]是否等于p[k+1]，next[i]都是等于k;
 *     对于优化后的next[i]，如果p[i]不等于p[k+1],则next[i]=k,反之,next[i]=0.

 * 这题的next[]是从0求到n,有n+1个值，因此对于next[i]=k的意义（0除外）就为：字符串下标为i的前k-1个字符与字符串头k个字符相等(上面提到的next[i]是与前k个字符与头k个字符相等next[i]才等于k)。
 * 对于长度为i个字符串，i-next[i]（满足i % （i-next[i]）==0)代表的意义就是 长度为i的字符串 的 最小循环子串的长度
 *  因此 字符串中存在周期的子串的最大循环次数=i/ (i-next[i]);
 *